MIT Linear Algebra, Lecture 3: Matrix Multiplication and Inverse Matrices

This is the third post in an article series about MIT's Linear Algebra course. In this post I will review lecture three on five ways to multiply matrices, inverse matrices and an algorithm for finding inverse matrices called Gauss-Jordan elimination.

The first lecture covered the geometry of linear equations and the second lecture covered the matrix elimination.

Here is lecture three.

Lecture 3: Matrix Multiplication and Inverse Matrices

Lecture three starts with five ways to multiply matrices.

The first way is the classical way. Suppose we are given a matrix A of size mxn with elements a_ij and a matrix B of size nxp with elements b_jk, and we want to find the product A·B. Multiplying matrices A and B will produce matrix C of size mxp with elements .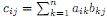

Here is how this sum works. To find the first element c₁₁ of matrix C, we sum over the 1st row of A and the 1st column of B. The sum expands to c₁₁ = a₁₁·b₁₁ + a₁₂·b₂₁ + a₁₃·b₃₁ + ... + a_1n·b_n1. Here is a visualization of the summation:

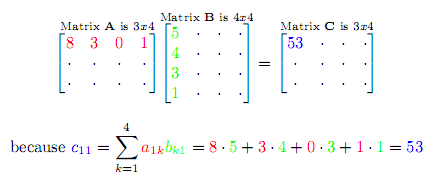
We continue this way until we find all the elements of matrix C. Here is another visualization of finding c₂₃:

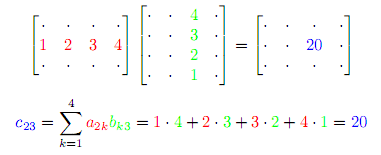
The second way is to take each column in B, multiply it by the whole matrix A and put the resulting column in the matrix C. The columns of C are combinations of columns of A. (Remember from previous lecture that a matrix times a column is a column.)

For example, to get column 1 of matrix C, we multiply A·(column 1 of matrix B):

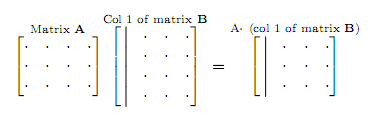
The third way is to take each row in A, multiply it by the whole matrix B and put the resulting row in the matrix C. The rows of C are combinations of rows of B. (Again, remember from previous lecture that a row times a matrix is a row.)

For example, to get row 1 of matrix C, we multiply row 1 of matrix A with the whole matrix B:

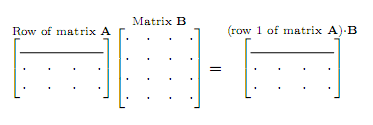
The fourth way is to look at the product of A·B as a sum of (columns of A) times (rows of B).

Here is an example:

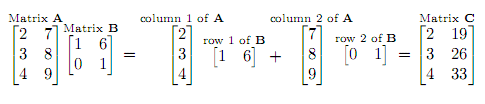
The fifth way is to chop matrices in blocks and multiply blocks by any of the previous methods.

Here is an example. Matrix A gets subdivided in four submatrices A₁ A₂ A₃ A₄, matrix B gets divided in four submatrices B₁ B₂ B₃ B₄ and the blocks get treated like simple matrix elements.

Here is the visualization:

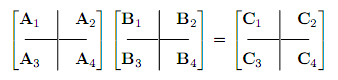
Element C₁, for example, is obtained by multiplying A₁·B₁ + A₂·B₃.

Next the lecture proceeds to finding the inverse matrices. An inverse of a matrix A is another matrix, such that A^-1·A = I, where I is the identity matrix. In fact if A^-1 is the inverse matrix of a square matrix A, then it's both the left-inverse and the right inverse, i.e., A^-1·A = A·A^-1 = I.

If a matrix A has an inverse then it is said to be invertible or non-singular.

Matrix A is singular if we can find a non-zero vector x such that A·x = 0. The proof is easy. Suppose A is not singular, i.e., there exists matrix A^-1. Then A^-1·A·x = 0·A^-1, which leads to a false statement that x = 0. Therefore A must be singular.

Another way of saying that matrix A is singular is to say that columns of matrix A are linearly dependent (one ore more columns can be expressed as a linear combination of others).

Finally, the lecture shows a deterministic method for finding the inverse matrix. This method is called the Gauss-Jordan elimination. In short, Gauss-Jordan elimination transforms augmented matrix (A|I) into (I|A^-1) by using only row eliminations.

Please watch the lecture to find out how it works in all the details:

Topics covered in lecture three:

• [00:51] The first way to multiply matrices.
• [04:50] When are we allowed to multiply matrices?
• [06:45] The second way to multiply matrices.
• [10:10] The third way to multiply matrices.
• [12:30] What is the result of multiplying a column of A and a row of B?
• [15:30] The fourth way to multiply matrices.
• [18:35] The fifth way to multiply matrices by blocks.
• [21:30] Inverses for square matrices.
• [24:55] Singular matrices (no inverse matrix exists).
• [30:00] Why singular matrices can't have inverse?
• [36:20] Gauss-Jordan elimination.
• [41:20] Gauss-Jordan idea A·I -> I·A^-1.

Here are my notes of lecture three:

The next post is going to be about the A=LU matrix decomposition (also known as factorization).