Many people are surprised to learn that sed, a seemingly simple text filtering program, is actually Turing complete. This realization prompts the question: how can a text processing utility achieve such computational power? The answer lies in sed's fundamental operations. Essentially, sed functions as a miniature assembly language, equipped with a comparison operation, branching capabilities, and a temporary buffer. These features collectively enable sed to perform any computation that a Turing machine can, thereby granting it Turing completeness.
I first learned about this from Christophe Blaess. His proof is by construction – he wrote a Turing machine in sed (download turing.sed). As any programming language that can implement a Turing machine is Turing complete we must conclude that sed is also Turing complete.
Christophe offers his own introduction to Turing machines and a description of how his sed implementation works in his article Implementation of a Turing Machine as a sed Script.
Here is an example program for his sed Turing machine that increments a binary number. The program has the initial tape configuration on the first line of the program and the program itself below it. In this example, initial tape configuration is the binary number 10010111 (151) and the program increments it by one.
| 10010111 # State 0 0 R0 011R1 000R1 # State 1 1 L2 100R1 111R1 # State 2 2 1R3 201R3 210L2 # State 3 3 RF 300R3 311R3
To run this program save it to a file (download increment.tm) and run it through turing.sed as following:
$ sed -f turing.sed < example.tm
You'll get the following output:
(0) | |10010111 (0) |1|0010111 (1) 1|0|010111 (1) 10|0|10111 (1) 100|1|0111 (1) 1001|0|111 (1) 10010|1|11 (1) 100101|1|1 (1) 1001011|1| (1) 10010111| | (2) 1001011|1| (2) 100101|1|0 (2) 10010|1|00 (2) 1001|0|000 (3) 10011|0|00 (3) 100110|0|0 (3) 1001100|0| (3) 10011000| | (F) 10011000 | | Final state F reached... end of processing
The output shows the state and tape changes as the program is executed. When it's done, the final state F is reached and the computation process terminates producing 10011000 (152) as a result, as expected.
Christophe isn't the first person to realize that sed is almost a general purpose programming language. People have written tetris, sokoban and many other programs in sed. Take a look at these:
Impressive and mind stretching!
 Alan Turing can't believe sed is Turing complete.
Alan Turing can't believe sed is Turing complete.
The Busy Beaver
If you liked this article, you'll also like my article about the busy beaver. The busy beaver is a Turing machine that puts 1's on an initially blank tape. The goal is to find an n-state Turing machine that puts as many 1's on the tape as possible. It hasn't been solved for a 5-state Turing machine yet and theorists doubt that it shall ever be computed for 6 states. I implemented this Turing machine and also wrote a program that visualizes tape changes.
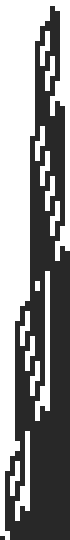 Busy beaver tape changes.
Busy beaver tape changes.
My sed book
I'm a huge fan of Unix tools and I wrote a fun little book about sed called Sed One-Liners Explained. If you don't know sed yet and want to learn it, my book teaches it through 100 practical and well-explained examples. As you work through them you'll rewire your brain to "think in sed." In other words, you'll learn how to manipulate the pattern space, hold buffer, input stream and output stream and you'll know how to get the results that you need. Take a look!
 sed book
sed book
I'll be writing many more interesting articles about Unix utilities and computation. Stay tuned and until next time!
