I'm currently messing with genetic algorithms. They are super fun and can be used to find optimal solutions to various physics problems and optimization problems in general. One of the problems I'm solving is simulating equilibrium configurations of two dimensional dipole systems of particles, which can attract and repel. This problem is NP hard, which means there is no effective algorithm to find the exact solution in an adequate time. A couple of algorithms can be used to approximate the solution and find near-equilibrium configurations, one of them being genetic algorithms.
The easiest situation is when the particles are bounded by a circle, which border they can't trespass. The goal is to find how these particles will position themselves inside this circle.
This case has already been solved using the simulated annealing method and near-optimal solutions for hundreds of particles have been found. This method uses different principles than genetic algorithm method, which I will describe shortly. The main idea of simulated annealing method is that the system is given an initial temperature which basically controls how much the particles will fluctuate inside the system. The greater the temperature, the bigger the fluctuations. The temperature gradually gets decreased and the fluctuations get smaller and smaller. Calculating the energy of the system and requiring it to be minimal at each step the temperature gets decreased eventually leads to a solution.
Here is how the solutions for 10, 11, 12, 13, 14 and 15 particles looks like, found using simulated annealing algorithms:
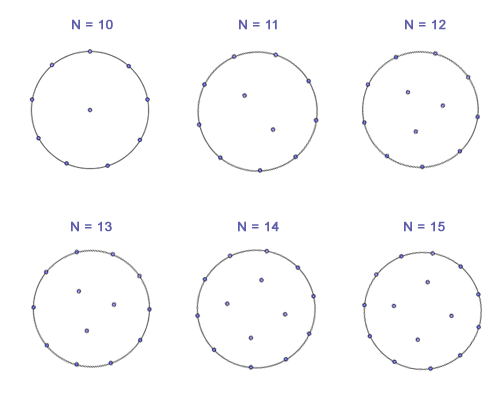
Notice how the particles position themselves in a case when another particle gets added to a system of 12 particles. Instead of positioning the new particle somewhere in the middle as in transition from 11 particles to 12, the system decides to put it on the border.
Here is a general description of what genetic algorithms are.
Genetic Algorithms 101
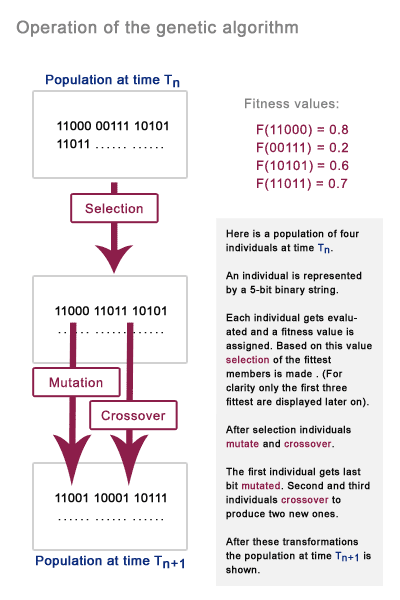
Genetic algorithms mimic the evolution by natural selection. The basic idea of genetic algorithms is very simple. Genetic algorithms feature populations of individuals which evolve with the use of the principles of selection, variation and inheritance.
One of the ways to implement this idea in computer programs is to represent individuals as strings of binary digits. Each bit in the string represents one gene. Each individual is assigned a numerical evaluation of its merit by a fitness function. The fitness function determines how each gene of an individual will be interpreted and, thus, what specific problem the population will evolve to solve.
Once all individuals in the population have been evaluated, their fitness values are used for selection. Individuals with low fitness get eliminated and the strongest get selected. Inheritance is implemented by making multiple copies of high-fitness individuals. The high-fitness individuals get mutated and they crossover to produce a new population of individuals. Mutation is implemented as flipping individual bits in the binary string representation of an individual and crossover happens as an exchange of binary substrings of two individuals to obtain a new offspring.
By transforming the previous set of individuals to a new one, the algorithm generates a new set of individuals that have better fitness than the previous set of individuals. When the transformations are applied over and over again, the individuals in the population tend to represent improved solutions to whatever problem was posed in the fitness function.
Here is an illustration of how a genetic algorithm might work: